Data Structure And Algorithms Interview Questions

Data structure and algorithm is one of the most important topics for efficient algorithm design and problem-solving and this makes DSA one of the most frequent topics for interviews. Let’s understand more about DSA interview questions.

Two types of Data structure and Algorithm questions are asked in interviews: theoretical and coding. And in this article, we will cover the Top 30 most frequently asked DSA interview questions for freshers and experienced.

Let’s begin!

DSA Interview Questions For Freshers

Question 1. What is a Data Structure?

Answer – A data structure is a storage way to organize data. The performance of tasks a program does depends on the type of data structure used. While designing an algorithm it is important to measure the pros and cons of different data structures according to their data insertion, retrieval, and deletion. Know what is data structure in detail.

Question 2. What are the different types of Data Structures?

Answer – Data structures are categorized into two different types:

• Linear data structure
• Non-linear data structure

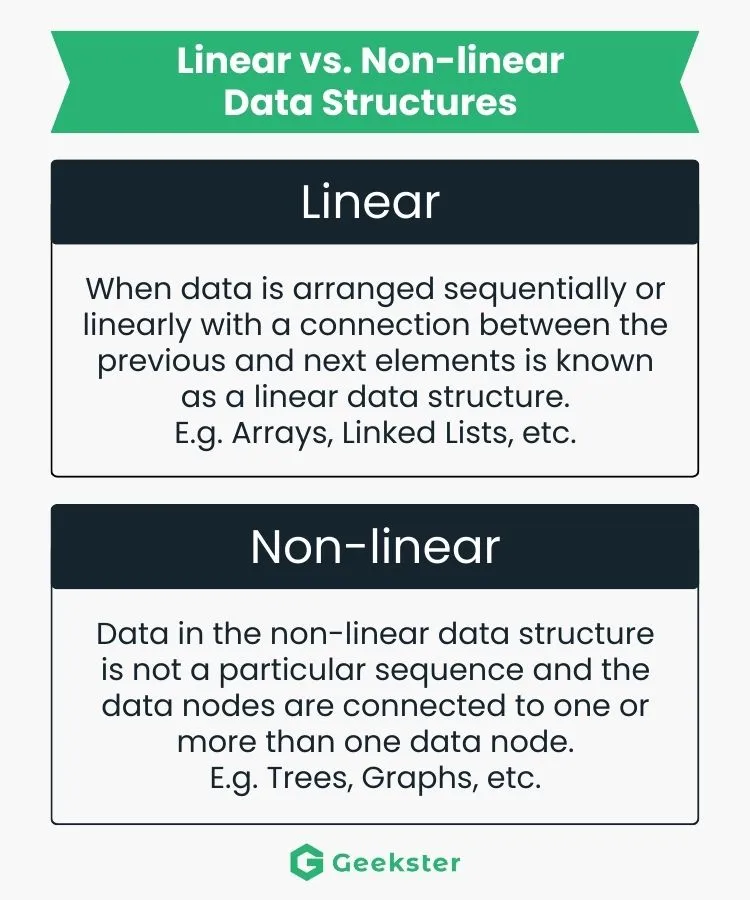
Question 3. What is the difference between Linear and Non-linear data structures?

• Linear Data Structure: When data is arranged sequentially or linearly with a connection between the previous and next elements is known as a linear data structure.
  E.g. Arrays, Linked Lists, etc.
• Non-linear Data Structure: Data in the non-linear data structure is not a particular sequence and the data nodes are connected to one or more than one data node.
  E.g. Trees, Graphs, etc.

Question 4. What is a Stack data structure? 

Answer – Stack is a linear data structure in which elements are stored in LIFO i.e. Last-In, First-Out order. 

If you have seen a stack of DVDs or clothes or books you already have a sense of its working i.e. to get a DVD out of a stack of DVDs we can only access what’s on top, similarly in a stack the access, adding or removing of an element can only be done from top and in a LIFO manner.

The stack data structure is really useful to keep track of the execution of an application. 

The applications of a stack data structure are:

• Postfix to Infix convertor
• Function calls order tracking
• Redo Undo feature in a document
• As temporary storage in recursive calls 

There are so many applications of the stack, what are some you can think of? 

Question 5. What are different operations available in stack data structure?

Answer – The different operations in a stack data structure are as follows: 

• Push: To add items in a stack we call push operation, which adds the item on the top of the stack. The famous Stack Overflow website is named after the Exception i.e. StackOverflowException which occurs when the stack is full and starts overflowing.
• Pop: To remove an element from the top of the stack we call the remove operation. The pop has an underflow condition when the stack becomes empty and hence no more elements to remove. In this case, the exception is the EmptyStackException. 
• Top: Top returns the item from the top of the stack.
• IsEmpty: It returns a boolean value, true in case of the empty stack or otherwise false.
• Size: It returns the size of the stack.

Question 6. What is a Queue data structure? 

Answer – A queue is a linear data structure in which elements are stored in FIFO i.e. First-In, First-Out order. A queue data structure can be observed as a queue of people waiting to get their movie tickets, the first customer who was added to the queue will get the ticket first and leave the front position from the queue and if a new person joins the queue they get added to the rear end of the queue. 

The applications of a queue data structure are:

• CPU Scheduling in a multiprogramming and time-sharing environment.
• Round Robin Scheduling
• Breadth-first search algorithms.
• Tasks with order maintenance like WhatsApp messages.

Question 7. What are different operations available in queue data structure?

Answer – The different operations in a queue in data structure are as follows: 

• enqueue: To add items in a queue we call the enqueue method, we add the item from the rear end of the queue. Overflow conditions occur when the queue is full.
• dequeue: To remove an element from the queue we call the dequeue method, we remove an element from the front of the queue. The dequeue has an underflow condition when the queue becomes empty.
• rear: It returns the rear element without removing it from the queue.
• front: It returns the front element without removing it from the queue.
• isEmpty: It returns the boolean value true in case of the empty queue or otherwise false. 
• size: It returns the size of the queue.

Question 8. Stack vs Queue data structure?

Answer –

STACK	QUEUE
Stack is a linear data structure in which elements are stored in LIFO i.e. Last-In, First-Out order.	Queue is a linear data structure in which elements are stored in FIFO i.e. First-In, First-Out order.
In Stack data is added and removed from the top.	Deletion in a Queue is called dequeue
Insertion in Stack is called push	Insertion in Queue is called enqueue
Deletion in Stack is called pop	Deletion in Queue is called dequeue
In Stack, only one single pointer is required for both push and pop.	In Queue, two pointers are required, one for deletion from the front and one for the addition at the rear.

Tip: Stack is used in solving recursion. And the queue is used in solving sequential and scheduling problems.

Question 9. What is a Linked List?

Answer – A linked list is a series of nodes where each node is connected to the next node. A singly linked list’s node has two important properties: data and the next node’s address. The data can be of any type or object.

• Each node in a Linked List denotes an entry. 
• The starting node is called the Head node and the last node in a Linked List is known as the Tail node.
• Head node points to the next node
• Tail node points to the null

The applications of a Linked List data structure are:

• Forward and Backward page operation in a browser
• Dynamic memory allocation 
• Implementation of Stack, Queue using Linked Lists.

Question 10. What are the different types of Linked Lists?

Answer – Linked Lists can be of various types: 

• Singly Linked List: A singly linked list data structure stores the data and connects the current node to the next node only. When we add a new data element to the singly linked list, the item gets added to a new node, and the node is added to the tail of the linked list which was earlier pointing to null. 

You can imagine a singly linked list as a node divided into two parts:

1. Part one contains the data 
2. Part two contains the address of the next node

• Doubly Linked List: A doubly linked list data structure stores the data in a new node and connects itself to the previous node and with the next node also. This helps in two-way accessing of data as each node points to the next and previous node. The main advantage that a doubly linked list serves is the ability to access a large amount of data back and forth. The main drawback of a doubly linked list is the memory cost as we need additional space for storing the previous node’s address/reference.

You can imagine a doubly linked list as a node divided into three parts:

1. Part one contains the address of the previous node
2. Part two contains the data 
3. Part three contains the address of the next node

• Circular Linked List: In a circular linked list, each node points only to the next node just like a singly linked list except tail node, the tail node that is the last node in a circular linked list points to the head node is the first node of the linked list and as a result, it forms a circular connection. 

• Doubly Circular Linked List: In a doubly circular linked list, each node points to the next node and as well as the previous node just like a doubly linked list but the tail node’s next is connected to the head and the head node previous is connected to the tail node.

Question 11. Is Linked List a Linear or Non-linear data structure?

Answer – A linked list is considered a linear data structure but if we discuss a linked list in terms of storage strategy that is a non-contiguous allocation of nodes, a linked list can be considered a non-linear data structure. Therefore, a linked list can be both a linear and non-linear type data structure. 

Question 12. Arrays vs Linked List Data structure?

Arrays	Linked List
A linked list is a collection of nodes. A node is divided into two parts i.e. data and an address	A Linked list is a collection of nodes. A node is divided into two parts i.e. data and an address
Array stores data elements in a continuous manner i.e. contiguous memory allocation	Linked list stores nodes in randomly available memory location i.e. non-contiguous memory allocation
Memory requirement for an array is fixed and cannot be changed during the runtime	Memory requirement for a linked list is decided during the runtime
Array elements are independent of the neighbour cells	Nodes in linked list are dependent on the previous and next node depending on the linked list type
Array provides constant time access for an element as all we require is the index for accessing	Accessing elements in a linked list takes more time as we need to iterate the linked list from head to tail for searching the element
Insertion and deletion take more time in array	Insertion and deletion are faster in linked list
Memory optimisation in the array is ineffective as the size of the array is fixed	Memory optimisation in the linked list can be done as we can free unwanted nodes

Question 13. How to implement Queue using Stack?

Answer – A queue can be implemented with the help of two stacks. 

Let the queue which is to be implemented be named queue and the stacks which we need to implement queue be stack1 and stack2. 

There are two ways we can implement a queue using two stacks:

• Making enqueue operation costly O(n):

– If we always keep the oldest element on top of stack1 so that if we dequeue, it can be done in O(1) time complexity. 

– To achieve this we need to use stack2 as temporary storage.

– STEPS:

1. enqueue O(n)

• while stack1 is not empty push everything from stack1 to  stack2

• Now push the new data to stack1
• Push back the data from stack2 to stack1

2. dequeue O(1)

• Pop the data from stack1 and return it
• If stack1 is empty return an error message

• Making dequeue operation costly O(n):

– For enqueue, we simply push new data to stack1 i.e. O(1) time complexity.

– For dequeue, if stack2 is empty, pop all the values from stack1 and push them to stack2 O(n).

– STEPS:

1. enqueue O(1)

• Push the new data to stack1

2. dequeue O(n)

• If stack2 is empty, pop all the values from stack1 and push them to stack2.
• Pop and return the value at the top of stack2
• If both the stacks are empty return the error message

Question 14. How to implement Stack using Queue?

Answer – A stack can be implemented with the help of two queues. 

Let the stack which is to be implemented be named stk and the queues which we need to implement stack be queue1 and queue2. 

There are two ways we can implement a stack using two queues:

• Making push operation costly O(n):

– If we somehow manage to keep the new data element in front of queue1 then the pop can be done in O(1) time complexity. 

– we use queue2 as a helper queue which will help in making sure new elements get added to the front of queue1. 

– STEPS:

3. push O(n)

• Enqueue the new data to queue2 
• Dequeue all the data from queue1 and enqueue to queue2
• Interchange the name of both the queues i.e. swap names 

4. pop O(1)

• Dequeue from queue1 and return it
• If queue1 is empty return an error message

• Making pop operation costly O(n):

– For push, we simply enqueue new data to queue1 i.e. O(1) time complexity.

– For pop, except the last data element, dequeue all the remaining data elements from queue1 and enqueue them to queue2 then dequeue and return the last remaining data of queue1. The time complexity of pop is O(n).

– STEPS:

1. push O(1)

• Enqueue the new data to queue1

2. pop O(n)

• Except for the last data element in queue1, dequeue all the data and enqueue them to queue2
• Dequeue the last data element from queue1 and store it as a result
• Interchange the names of both the queues so that queue1 becomes queue2 and vice versa
• Return the result

Question 15. Explain the asymptotic analysis of an algorithm.

Answer – Asymptotic analysis tells us about the “run-time performance” of an algorithm in mathematical units. It helps in finding the best case, worst case, and average case time required for completing a task. Asymptotic analysis is essential for analyzing an algorithm’s efficiency.

Question 16. What is a HashMap data structure?

Answer – A HashMap data structure that stores data in the form of key-value pairs. As the key value suggests, the hash map stores some value for a corresponding key. The accessing in Hash Map is of ~ O(1). 

For accessing a certain value in a hashmap we need to know the key and the key should exist in the hashmap. The keys in a hashmap are unique identifiers, so if you want to insert another value with the same key the new value will replace the older stored value.

Question 17. How are HashMap collisions handled in Java?

Answer – A collision occurs when a compress function gives the same output for two different inputs. In the case of collision, we do collision handling. 

Collision handling can be done in two ways:

• Closed addressing
• Open Addressing

In older versions of Java, collisions are handled by chaining, that is when more values get added in the same bucket due to different keys ending up being in the same bucket, we add those values in a linked list that is stored in that bucket. 

The retrieval of data can go up to O(n) in the worst case as all the values can end up being in the same bucket, to reduce the access time, in Java 8, when the number of entries in a bucket becomes more than 8 then instead of a linked list, the balanced tree is used so that the access time in the worst case is O(log n) instead of O(n). 

Question 18. What is the time complexity of basic operations in the HashMap?

Answer – The time complexity in HashMap depends on the hashing function. If the hashing function is efficient with uniform distribution of elements in the buckets, the time complexity for put() and get() becomes O(1).

DSA Interview Questions for Experienced 

Question 19. What is a tree data structure?

Answer – A generic tree is a non-linear hierarchical data structure made up of multiple nodes that have parent-child relationships between them. 

Every non-empty tree has a root node which is also referred to as a level 0 node and the rest of the nodes are children and grandchildren of the root node.

Root node references to the children nodes and each children node references to their child nodes.

A tree can be divided into smaller subtrees.

Question 20. Why is Tree a non-linear data structure?

Answer – In a tree, data is not stored in a linear fashion rather the data is stored in a hierarchical or multilevel manner and this is why trees are non-linear data structures.

Question 21. What are the basic terminologies in a Tree data structure?

Answer – The basic terminologies in a Tree data structure are:

• Root Node: The root node is the topmost node in a tree, and for an empty tree, the root is said to be null. A root node does not have any parent node. 
• Parent Node: The parent node is the predecessor of a node, which means the parent node will have reference to the child node directly.
• Child Node: A child node is the immediate successor of a node. 
• Leaf Node: If a node doesn’t have any child node then it is said to be a leaf node.
• Sibling: Children nodes of the same parent node are called sibling nodes.
• Cousin: Nodes that are at the same level but whose parents are different are called cousin nodes. 
• Level of a Node: The level of a node denotes the total count of edges required from the root to reach a particular node.
• Number of Edges: Edge is the representation of the connection between two nodes, the parent node, and connected to a child node via edge. If a tree has N nodes then the tree will have N-1 edges.
• Depth of a Node: The length of the path from the root to a particular node is called the depth of a node. It can be calculated by calculating the number of edges from the root to that node. 
• Height of a Tree: The height of a tree is calculated by finding the longest path from the root to the leaf node.
• Degree of a Node: The degree of a node is the count of the total number of edges going through that particular node to its children. It can also be said the total number of subtrees attached to a node is called the degree of a node.

Question 22. What is a Binary Tree data structure?

Answer – Binary Tree is a type of tree where each node can have 0, 1, or a maximum of 2 children. 

A binary tree is used for efficient storage retrieval and manipulation of data. In a binary tree, each node has at most two children.  For a parent node, the children can be referred to as the left child and right child, and these children are known as siblings. 

Question 23. What is a Complete Binary Tree?

Answer – A complete Binary Tree is a binary tree in which all the levels except the last level should be completely filled i.e. should have both the children and the filling of elements should be from the leftmost position.

Question 24. What are the different types of traversal in trees?

Answer – There are usually three ways to traverse a tree:

• Inorder Traversal:  The order of traversal for inorder traversal is left subtree then root and then right subtree. Steps for Inorder Traversal: 
  • Make a recursive call on the left subtree i.e. root.left
  • Do operation on the root node
  • Make a recursive call on the right subtree i.e. root.right

• Preorder Traversal:  The order of traversal for preorder traversal is root then left subtree and then right subtree. Steps for Preorder Traversal: 
  • Do operation on the root node
  • Make a recursive call on the left subtree i.e. root.left
  • Make a recursive call on the right subtree i.e. root.right

• Postorder Traversal:  The order of traversal for postorder traversal is left subtree then right subtree and then root. Steps for Inorder Traversal: 
  • Make a recursive call on the left subtree i.e. root.left
  • Make a recursive call on the right subtree i.e. root.right
  • Do operation on the root node

Question 25. What is a Binary Search Tree (BST) data structure

Answer – Binary search tree (BST) is just like Binary Tree but with additional conditions:

• All the elements on the left subtree should be less than or equal value when compared to the parent node.
• All the elements on the right subtree should be greater than or equal in value when compared to the parent node.
• Above two rules are applicable to all the nodes in a Binary Search Tree.

Searching for an element in BST is of O(log(h)) where h is the height of the tree. Binary search trees are beneficial when we want to store sorted data in a tree format. Inorder traversal in a BST gives nodes in ascending order.

Question 26. What is Heap data structure?

Answer – Heap is a Binary Tree based data structure, and the tree should be a completely balanced binary tree.

Heaps are of two types:

• Min Heap: In min heap, the value of the parent node should be less than or equal to the children nodes. The root is the minimum value among all the other values.
• Max Heap: In a max heap, the value of the parent node should be greater than or equal to the children nodes. The root is the maximum value among all the other values. 

In Heap, this structure is maintained through a special operation called Heapify. It is a process of creating a heap. The insertion and deletion in a heap take place in O(log N). To check the minimum value in the min heap or maximum value in the max heap is called peek. It is of O(1) time complexity.

Priority Queue can be implemented using a heap data structure.

Question 27. What is a graph data structure?

Answer – A Graph is a non-linear data structure constitute of nodes and edges connecting those nodes. In a graph, the nodes are also called vertices. 

The Graph data structure can be categorized into various different types, some of them are connected and disconnected graphs, weighted graphs, directed and undirected graphs, and more.

The iteration in a graph can be done in two ways Breadth First Search (BFS) and Depth First Search (DFS).

A graph can be represented primarily in two ways:

• Adjacency Matrix
• Adjacency List

Question 28. Discuss the comparison between the Adjacency Matrix and Adjacency List representation of the Graph.

Answer – Since a Graph is a non-linear data structure consisting of nodes and edges, we need a way to store the nodes/ vertices and edges connecting them. 

This can be achieved primarily in two ways:

• Adjacency Matrix
• Adjacency List

Let’s quickly discuss them.

1. Adjacency Matrix: Adjacency matrix in a 2-Dimensional array of size VxV where V is the number of nodes or vertices in a graph. So if we want to show an edge between vertex 2 and vertex 4 we can do it by adj[2][4] = 1 and adj[4][2] = 1   

adj[2][4] = 1 represents the matrix named adj and an edge connection between vertex 2 and 4. In order to make a directed graph edge representation connection starting from vertex 2 to vertex 4 and not 4 to 2 is represented by adj[2][4] = 1 and adj[4][2] = 0. A general way of representing this is adj[i][j] = weight, where i and j are vertices and weight, is the weight of the edge (1 in the case of a simple graph).

2. Adjacency List: An adjacency List is an array with addresses of the lists the list can be LinkedList or any other list based on the requirement. The index of the array represents the vertex and the node in the list represents a connection between those vertices. Adjacency lists can also represent the weighted graphs by modifying the lists.

Let’s consider the graph below and represent it using the Adjacency matrix and Adjacency list.

• Adjacency Matrix representation

• Adjacency List representation

Question 29. Differentiate between Breadth First Search (BFS) and Depth First Search (DFS).

Breadth First Search (BFS)	Depth First Search (DFS)
In BFS we iterate through all the nodes at a particular level first and then we go to the next level	In DFS we iterate through the depth of the graph or a tree i.e. reaches the farthest point from origin or root node
BFS is done using queue data structure	DFS is performed using stack data structure
BFS is preferable when the target is closer to the starting node	DFS is preferred when the target is far from the starting node
BFS is based on FIFO i.e. First In, First Out	DFS is based on LIFO i.e. Last In, Last Out
If a node is visited in BFS multiple times it is removed from the queue	Visited nodes are added to the stack and then they are removed
BFS doesn’t facilitate backtracking	DFS is a recursive algorithm and hence backtracking can be done in DFS

Question 30. What is the application of the graph data structure?

Answer – Graph is one of the most important data structures with applications in various different domains, it is used to implement Google Maps, Facebook’s friend suggestion algorithm, and find mutual friends algorithm. The graph is used widely on social media sites to store user data in order to run many relation-based algorithms. 

In the Data domain DAG i.e. Directed Acyclic Graph is used some of the tools which use DAG are MS Excel and Apache Airflow.

In the world, wide web websites can be considered as vertices on a graph and there are edges between them.

In this article, we quickly revised the top 30 most frequently asked Data Structure and Algorithms (DSA) Interview Questions for freshers to experience. Now all the best. May the force be with you! 🔥